Cite as:
Introduction to Pure See. © Marius Buliga (2020-2021), https://mbuliga.github.io/quinegraphs/puresee.html


Draft! Version 06.06.2020

See also:
All chemlambda projects



Pure See

is a geometrical, or cartographical lambda calculus. As primitives it uses variables, terms and a small number of special words: from, see, as, in, apply, with, note, over, free, origin.

Contents

Scalars

Variables and terms

Commands

Conversion between commands, functional and algebraic forms

Reduction of trigrams

Multiplication by scalars. Origin

Reduction by passing to the limit

Emergent rewrites





Scalars

(back to contents)

The following special words are scalars: from, see, as, in, apply, with, note, over. They are rational functions of a formal parameter denoted usually by "z":
special word as a rational function
see see[z] = z
from from[z] = 1-z
apply apply[z] = 1/z
with with[z] = 1/(1-z)
note note[z] = z/(z-1)
over over[z] = (z-1)/z
as as[z] = -1
in in[z] = 1
There are three special scalars. The scalar "in" is also denoted by "1". The two other special scalars are: 0 (which can be seen as the constant rational function equal to 0) and ∞. Any number of other constant functions may be considered as scalars.

These scalars (with the exception of those special ones) generate all the scalars via two operations: composition of scalars and multiplication of scalars.

Composition of scalars is defined as composition of functions

k[l][z] = k[l[z]], for k,l scalars

Remark that with composition the set {see, from, apply, with, note, over} is the anharmonic group. This group is isomorphic with the group of permutations of 3 elements.

Multiplication of scalars is defined as multiplication of functions

[k l][z] = k[z] l[z], for k,l scalars

Composition and multiplication of scalars 0 and ∞ with any other scalar is undefined.

Variables and terms

(back to contents)

Variables are denoted by a, b, c, ... A term is either a variable or the result of an operation between terms. There are 6 operations: ◦ is "map" , • is "unmap", (lambda calculus style) abstraction, (lambda calculus style) application, > is "fi", < is "fox". All in all, a term is defined as:

origin | (is asimilated with a variable)
a variable |
a ◦ b a, b terms | (map)
a • b a, b terms | (unmap)
a > b a, b terms | (fi)
a < b a, b terms | (fox)
λ a. b a, b terms | (abstraction)
a b   b, b terms | (application)


Commands

(back to contents)

Pure See uses mainly 6 commands, which correspond to the 6 operations. Each operation is an "algebraic form" of the associated command. There are several other commands, which don't have a functional form.

As indicated in the images, each command can be associated to a directed interaction combinators (dirIC) node, as defined in:
[Alife properties of directed interaction combinators vs. chemlambda. Marius Buliga (2020), https://mbuliga.github.io/quinegraphs/ic-vs-chem.html#icvschem]
or a chemlambda [arXiv:2003.14332] node.

For the list of chemlambda rewrites and the history of versions see
[Graph rewrites, from emergent algebras to chemlambda. Marius Buliga (2020), https://mbuliga.github.io/quinegraphs/history-of-chemlambda.html]

The exceptions are the nodes named "D" and "FOX", first time used in kali24 (but see them described in the file chemistry.js) and the node "FIN", the fanin dual to the fanout FO.

command algebraic form functional form graphical form

from e see a as b;

map

b = e ◦ a;

from e see a as b;

from e see a as b

see a from e as b;

 abstraction

b = λ e. a;

see a from e as b;
see a from e as b

as b from e see a;

 application

a = b e;

apply b over e as a;
as b from e see a

see a as b from e;

 fi

e = a > b;

note a with b as e;
see a as b from e

from e as b see a;

 unmap

a = e • b;

over e apply b as a;
from e as b see a

as b see a from e;

 fox

e = b < a;

with b note a as e;
as b see a from e
There are several supplementary commands: fanout and fanin:

in e as a free b;

in e as a free b

in e free b as a;

in e free b as a
an Arrow command:

in a as b;

and an input, output and free commands:

in a;

as a;

free a;

which correspond respectively to 1-valent nodes denoted respectively by FROUT, FRIN and T.

Conversion between commands, functional and algebraic forms

(back to contents)

The functional form of a command is the command multiplied by a scalar.Example:

apply b over e as a;

is the command as b from e see a; multiplied by the scalar apply as, i.e.

(apply as) (as b from e see a);

We can pass from algebraic forms to commands by the following rewrite (ALG):

b = a; is replaced by in a as b;
Examples:

command algebraic form replace by
from e see a as b; b = e ◦ a; in (e ◦ a) as b;
see a from e as b; b = λ e. a; in (λ e. a) as b;
as b from e see a; a = b e; in (b e) as a;
see a as b from e; e = a > b; in (a > b) as e;
from e as b see a; a = e • b; in (e • b) as a;
as b see a from e; e = b < a; in (b < a) as e;
Another rewrite is (COMB) which eliminates Arrow commands:
LHS pattern action
in a as b; delete the command,
replace b by a
with the exception: delete in a as a;

(ALG) and (COMB) may be combined into an evaluation rewrite (EVAL), for example
LHS pattern action
see a from e as b; delete the command,
replace b by λ e. a

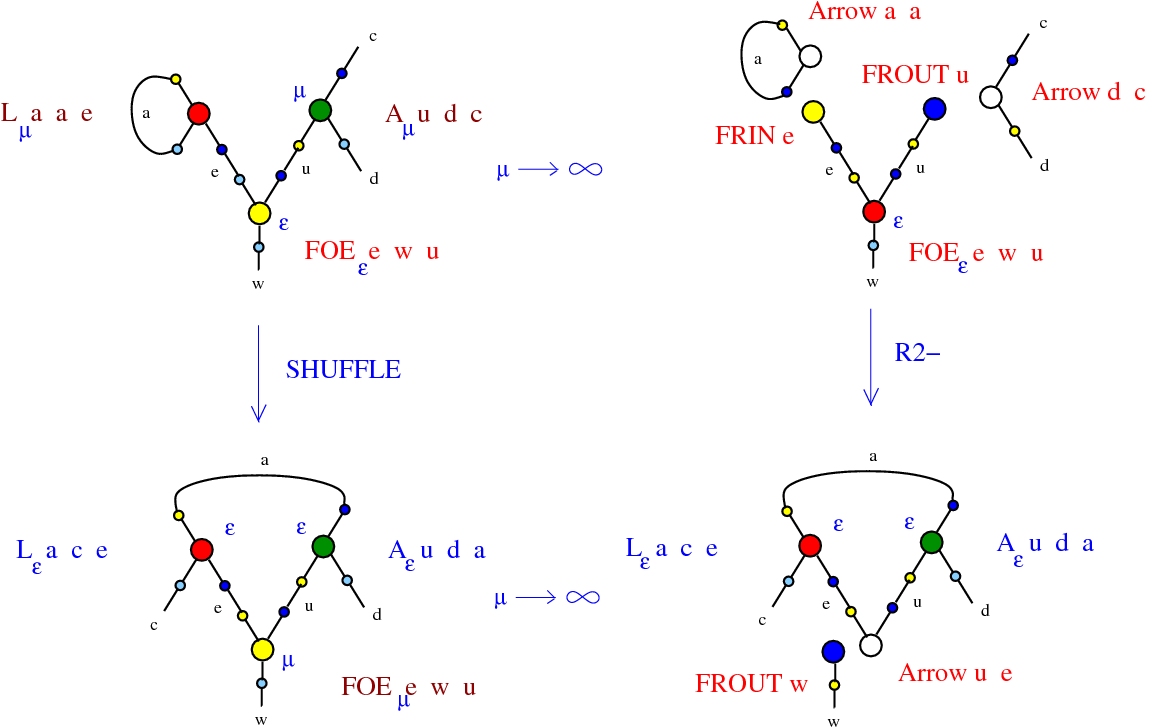
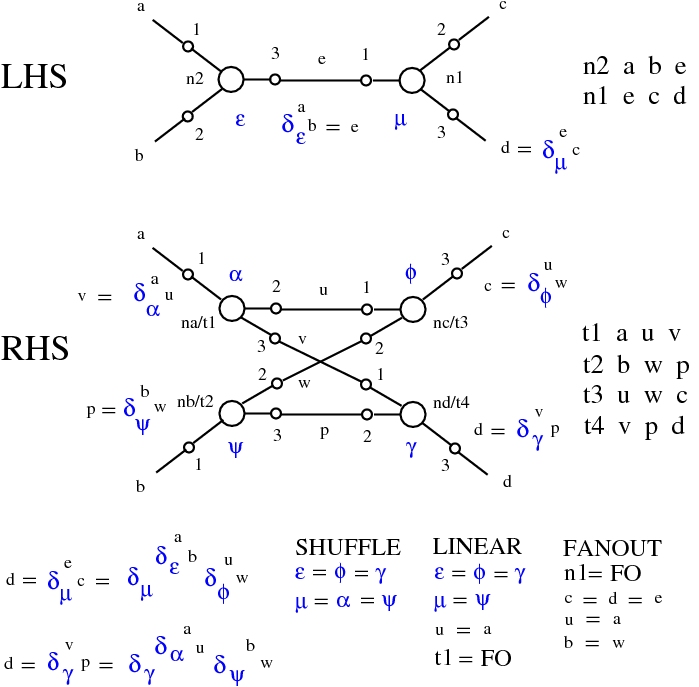
Reduction of trigrams

(back to contents)

A trigram is any triple of commands of the form:
for[ε] a see[ε] b as[ε] e;
for[μ] e see[μ] c as[μ] d;
for[ε] u see[ε] w as[ε] c;
where μ, ε are scalars.

The main rewrite (schema) of Pure See is (SHUFFLE), which replaces a trigram by another trigram:
LHS pattern RHS pattern
from[ε] a see[ε] b as[ε] e;
from[μ] e see[μ] c as[μ] d;
from[ε] u see[ε] w as[ε] c;
from[μ] a see[μ] u as[μ] v;
from[ε] v see[ε] p as[ε] d;
from[μ] b see[μ] w as[μ] p;
trigram for a DIST1

Multiplication by scalars. Origin

(back to contents)

The special word origin is a term. With respect to the origin we define the multiplication by the scalar μ of the term T:

from[μ] origin see[μ] T as (μ T);

The multiplication of a command

from[ε] u see[ε] w as[ε] c;

by the scalar μ is defined as

from[ε] (μ u) see[ε] (μ w) as[ε] (μ c);

via a SHUFFLE schema
LHS pattern RHS pattern
from[ε] origin see[ε] origin as[ε] origin;
from[μ] origin see[μ] c as[μ] (μ c);
from[ε] u see[ε] w as[ε] c;
from[μ] origin see[μ] u as[μ] (μ u);
from[ε] (μ u) see[ε] (μ w) as[ε] (μ c);
from[μ] origin see[μ] w as[μ] (μ w);

Reduction by passing to the limit

(back to contents)

We are allowed to "pass to the limit" with scalars, to one of the special scalars 0, 1, ∞. This passage to the limit is a rewrite.

LHS pattern RHS pattern
from[μ] e see[μ] a as[μ] b; μ → 1 in e; in a as b;
μ → 0 in a; in e as b;
μ → ∞ in e free a as b;
see[μ] a from[μ] e as[μ] b; μ → 1 as e; in a as b;
μ → 0 in a as e free b;
μ → ∞ as b; in a as e;
as[μ] b from[μ] e see[μ] a; μ → 1 in e; in b as a;
μ → 0 in b free e as a;
μ → ∞ as b; in e as a;
see[μ] a as[μ] b from[μ] e; μ → 1 in a free b as e;
μ → 0 in a; in b as e;
μ → ∞ in b; in a as e;
from[μ] e as[μ] b see[μ] a; μ → 1 in e as b free a;
μ → 0 as a; in e as b;
μ → ∞ as b; in e as a;
as[μ] b see[μ] a from[μ] e; μ → 1 as e; in b as a;
μ → 0 as a; in b as e;
μ → ∞ in b; as a free e;

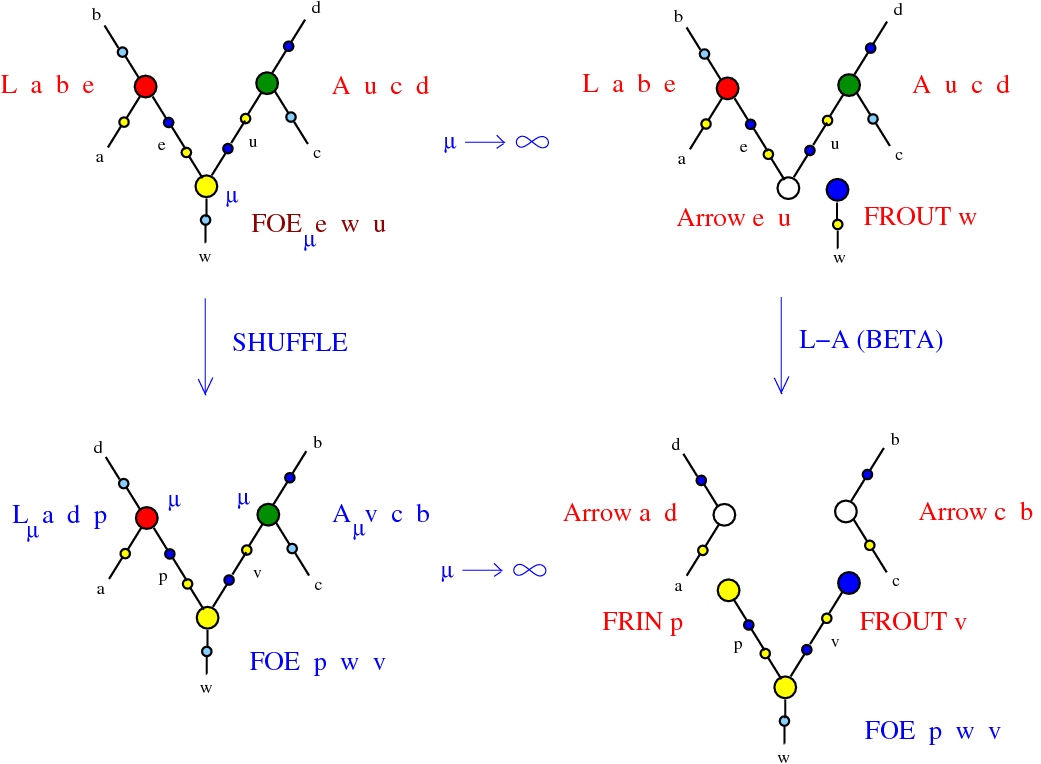
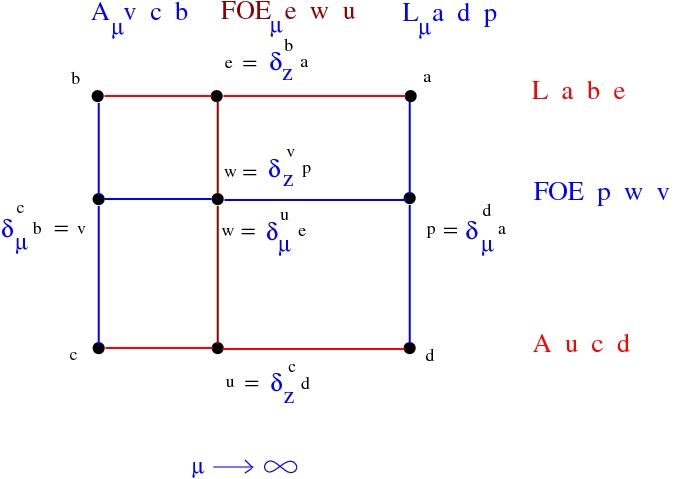
Emergent rewrites

(back to contents)

Here is exemplified the rewrite L-A (or the beta rewrite) as an emergent rewrite. You see the rewrite described in graphical form and in trigram form:
emergent BETA
trigram for LA
COMB rewrites are also applied.

Look in diagonal, from the top left to the bottom right of the figure which shows the graphical form of L-A as emergent. We may interpret the FOE node as the rewrite enzyme.

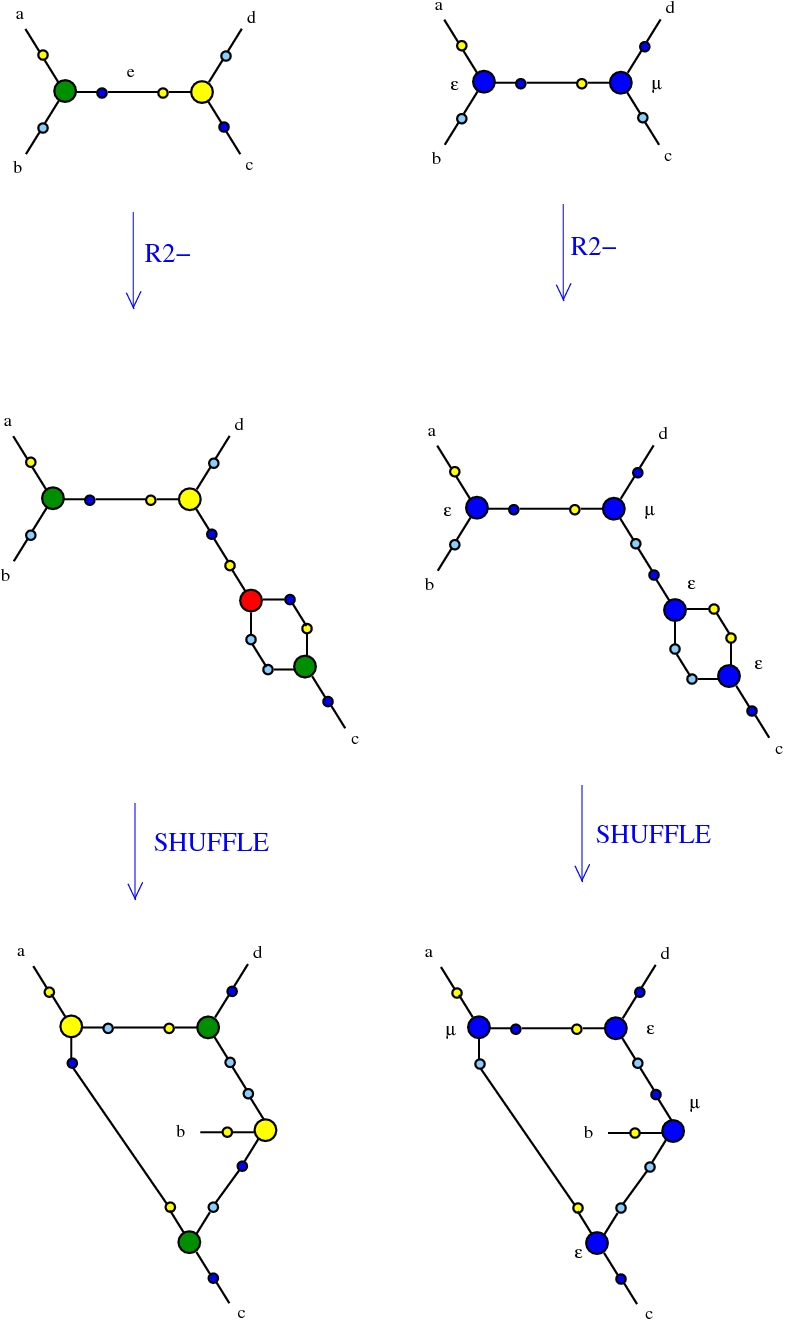
DIST rewrites of chemlambda, dirIC or even those of kali24 are described in the file chemistry.js. They are particular forms of the possible DIST rewrites which are compatible with the SHUFFLE. Here is a tool which generates all possible such rewrites.

Let's concentrate on the dist1 rewrite. The following figure shows the graphical form of this rewrite:

dist1 rewrite commented

In trigram form, the various nodes (i.e. commands) appear as lines:

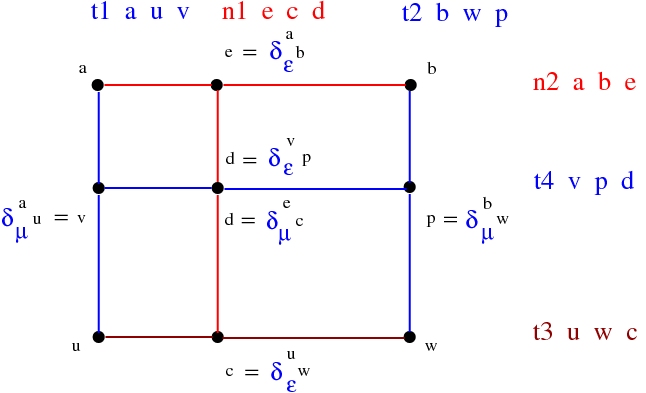
trigram for a dist1

But the LHS pattern of a dist1 has 2 nodes and the RHS pattern has 4 nodes. We can't use directly a SHUFFLE (which transforms 3 nodes into 3 nodes) in order to obtain this rewrite. We need first to create the term "c" (in the previous figure, the one which corresponds to the horizontal line from the bottom). Once created, this new line (i.e command) will allow the use of a SHUFFLE.

The creation of this new line can be achieved by an emergent Reidemeister 2 rewrite:

emergent R2-

And the SHUFFLE which finishes the dist1 rewrite is in the next figure. The right column of the figure shows the rewrite in terms of D nodes (dilations) and the column from the left shows the rewrite A-FOE from chemlambda, which is a particular dist1 rewrite.

emergent DIST1