Emergent rewrites in knot theory and logic
[video] [no js slides]
Marius Buliga (IMAR)
I explain in what sense new graph rewrite systems emerge from given ones, with two examples:
- • the emergence of the R3 (Reidemeister 3) rewrite from R1, R2 and some uniform continuity assumptions, and relations to curvature,
- • the emergence of the beta rewrite in lambda calculus from the shuffle rewrite and relations to the commutativity of the addition of vectors in the tangent space of a manifold
From sub-riemannian geometry to emergent algebras
A riemannian manifold (X,g) is a length metric space (X,d) by Hopf-Rinow thm.
Problem 1: recover (X,g) from (X,d).
- • (1935, A. Wald) problem 1 for 2-dim manifolds.
- • (1948, A.D. Alexandrov) a metric notion of (sectional) curvature + smoothness solves 2-dim manifolds.
- • (1982, A.D. Alexandrov) conjecture that the same is true for n-dim manifolds.
- • (1998, I.G. Nikolaev) proves (Alexandrov conjecture) for n-dim manifolds.
From sub-riemannian geometry to emergent algebras
but (1996, M. Gromov) asks for a solution of
Problem 2: recover sub-riemannian (X,D,g) from (X,d).
- • (X,D,g) sub-riemannian if D completely non-integrable distribution and g a metric on D.
- • by Hopf-Rinow (X,D,g) is a length metric space (X,d), with d the CC distance.
From sub-riemannian geometry to emergent algebras
Sub-riemannian spaces are weird! (except when riemannian)
- • metric (Hausdorff) dimension > topological dimension
- • not Alexandrov spaces
- • tangent spaces are nilpotent (Carnot) groups, not vector spaces
- • Carnot groups have a peculiar differential calculus (Pansu derivative)
From sub-riemannian geometry to emergent algebras
Sub-riemannian spaces (techniques) are useful!
- • (1981, M. Gromov) finitely generated groups of polynomial growth same as those groups which have nilpotent subgroups of finite index
- • (1989, P. Pansu) proves Rademacher thm for Carnot groups, which implies a short proof for Margulis-Mostow rigidity
- • (2006, J.R. Lee, A. Naor) counter-example to Goemans-Linial conjecture by using the Heisenberg group as a SR space
- • (2010, E. Hrushovski) (2011, E. Breuillard, B. Green, T. Tao) Approximate groups are essentially Carnot groups
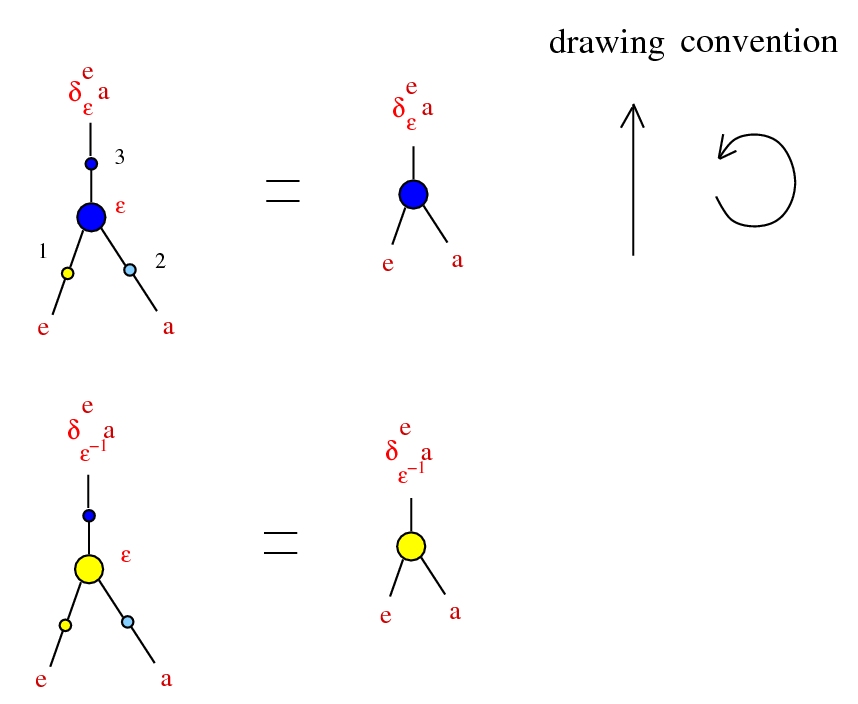
Drawing conventions
Emergent algebras
Used in: A characterization of sub-riemannian spaces as length dilatation structures constructed via coherent projections a solution of the problem of intrinsic characterization of sub-riemannian manifolds posed by M. Gromov, 1996.
introduced as algebras in arXiv:0907.1520, as a λ calculus in arXiv:1807.02058.
Emergent algebras

Emergent algebras
Emergent algebras

Emergent algebras

Emergent algebras
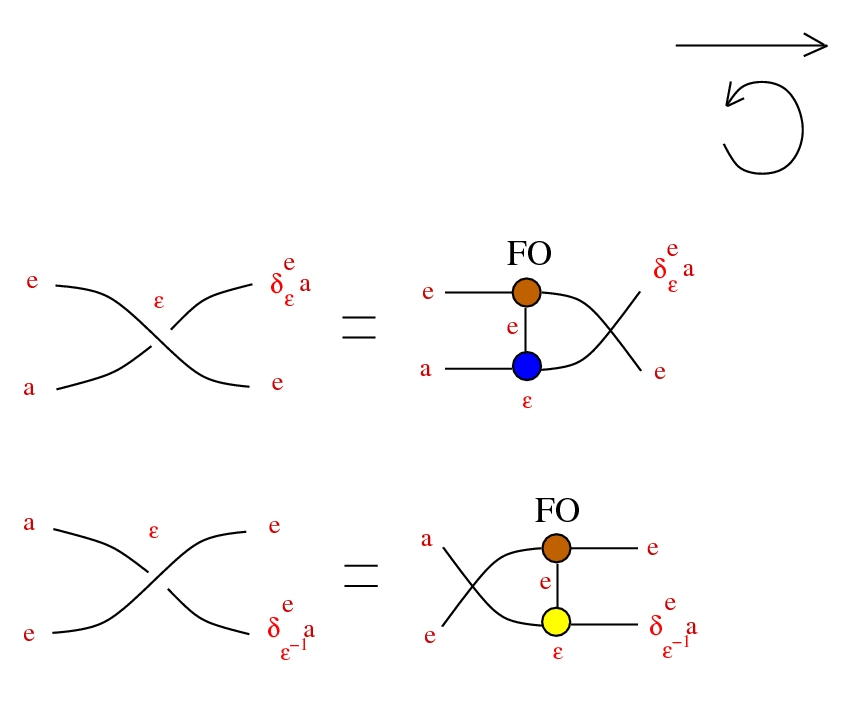
Drawing conventions 2
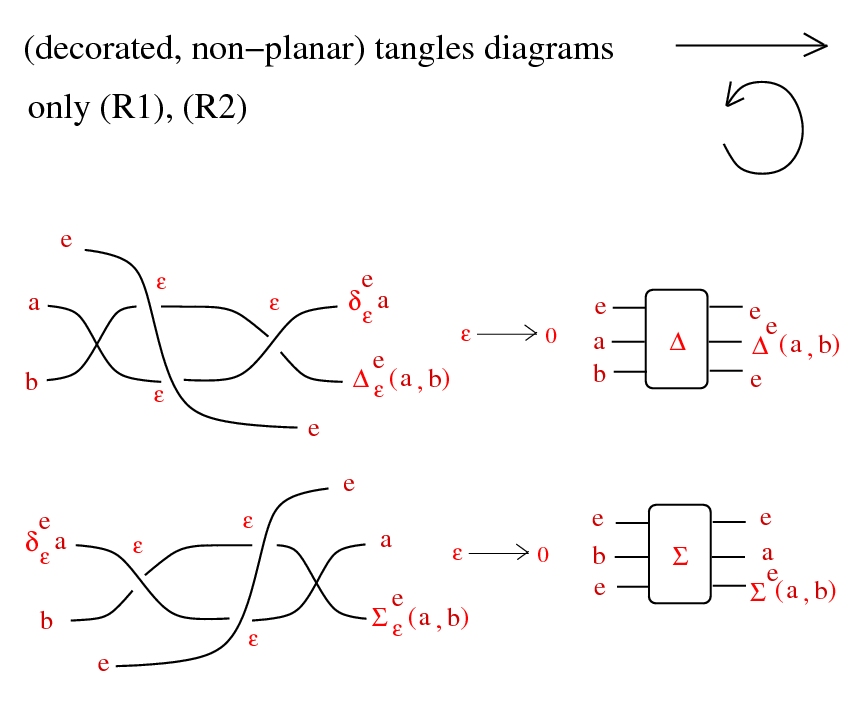
Tangles
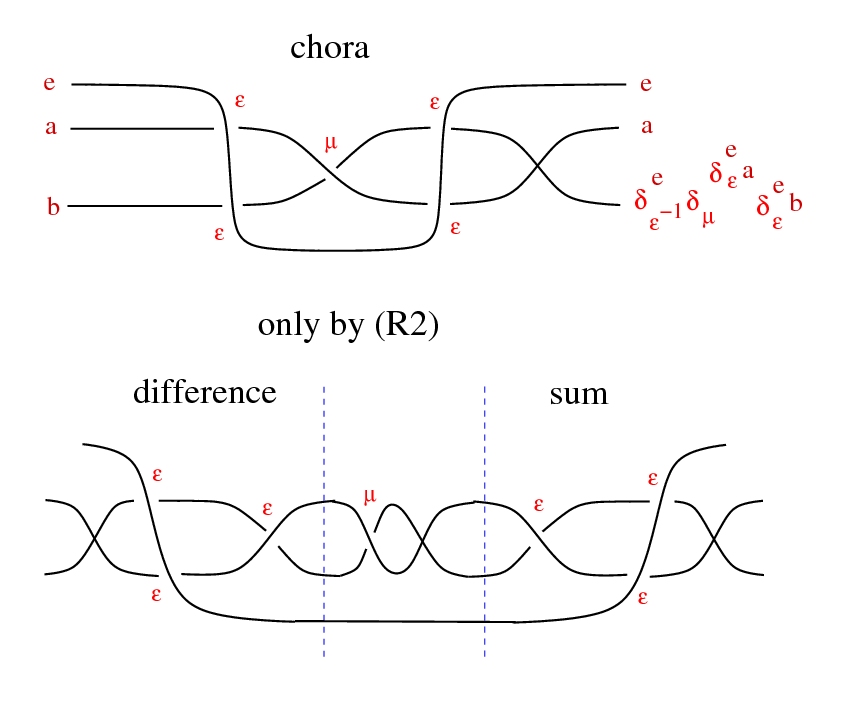
Chora
Chora
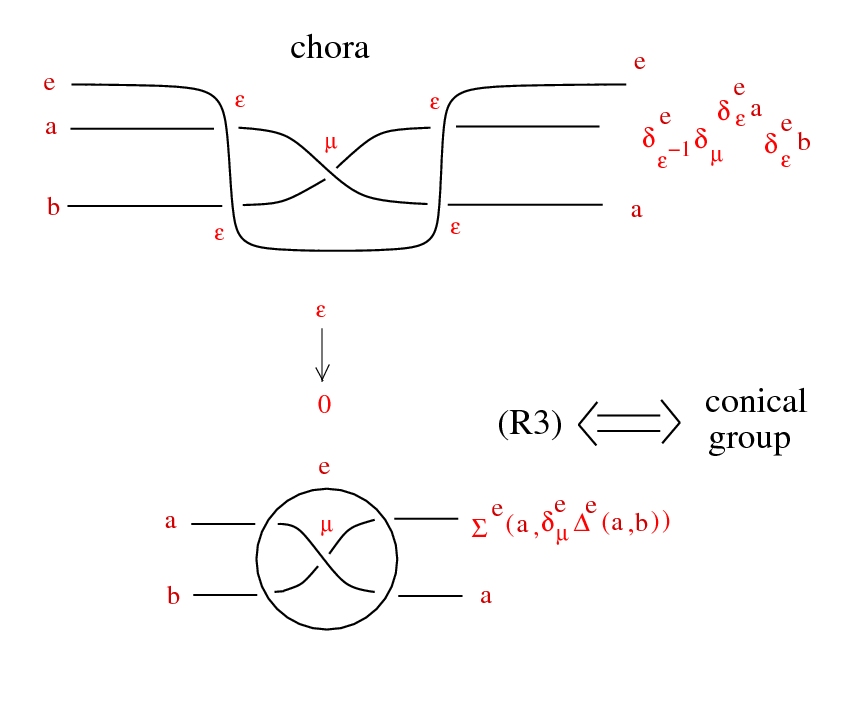
Conical groups
groups with:
an action by automorphisms
a ⋅ (x * y) = (a ⋅ x) * (a ⋅ y)
which are uniformly contractive:
ε → 0, ε ⋅ x → e, uniformly wrt x in compact set
an action by automorphisms
a ⋅ (x * y) = (a ⋅ x) * (a ⋅ y)
which are uniformly contractive:
ε → 0, ε ⋅ x → e, uniformly wrt x in compact set
Examples
- • (normed) finite dim vector space X, * = +, Γ = (0, ∞)
- • Heisenberg groups:
- - take (H, <,>) complex Hilbert space, X = H × R
- (x,u) * (y,v) = (x + y, u + v + (1/2) Im <x,y>)
- - distribution D from left translate of H in X, is completely nonintegrable
- - metric on D from Re <,>
- - Γ = C ∖ {0}
- a ⋅ (x,u) = (a x , ∣a∣² u )
- • or just any Carnot group
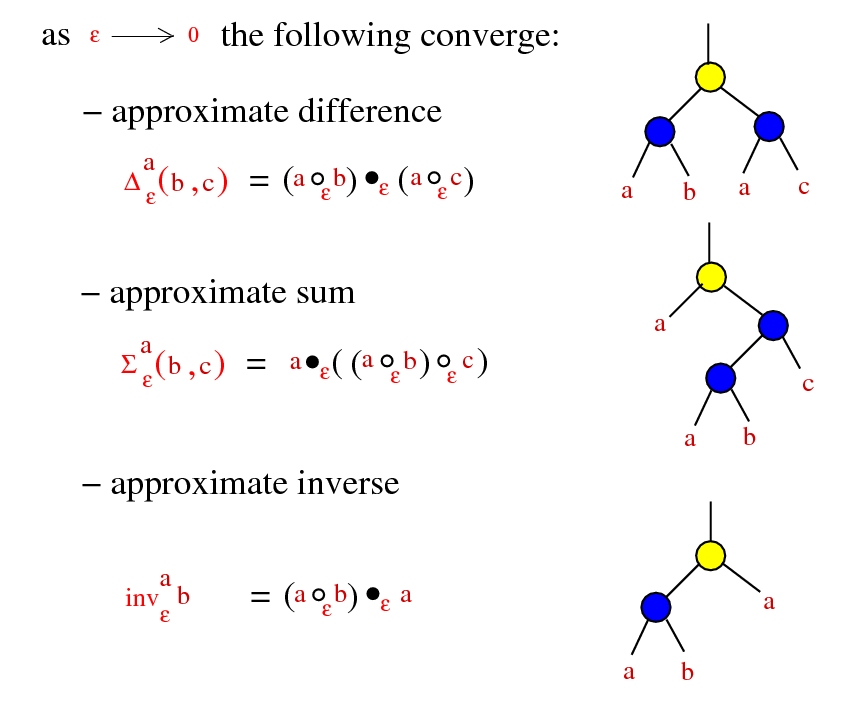
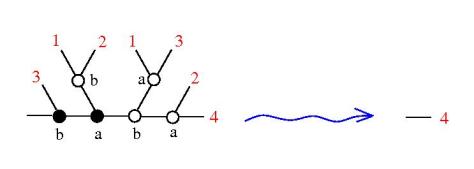
Tangles
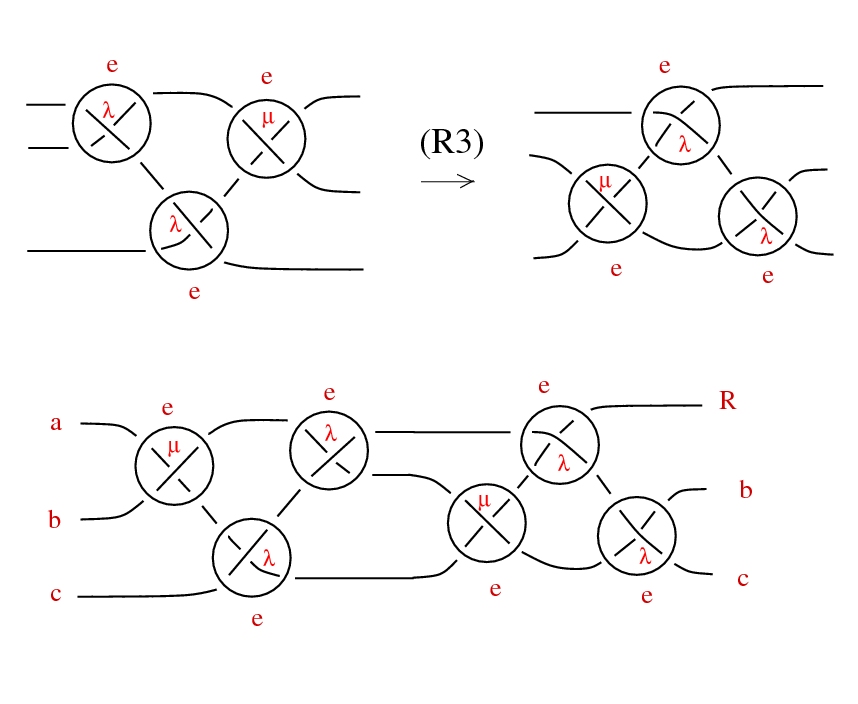
Rescale!
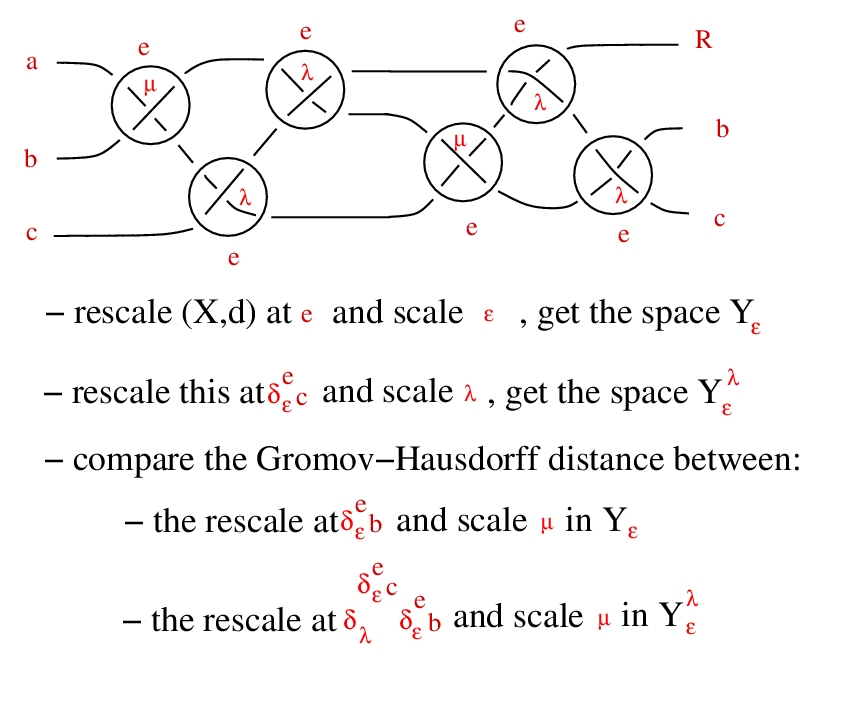
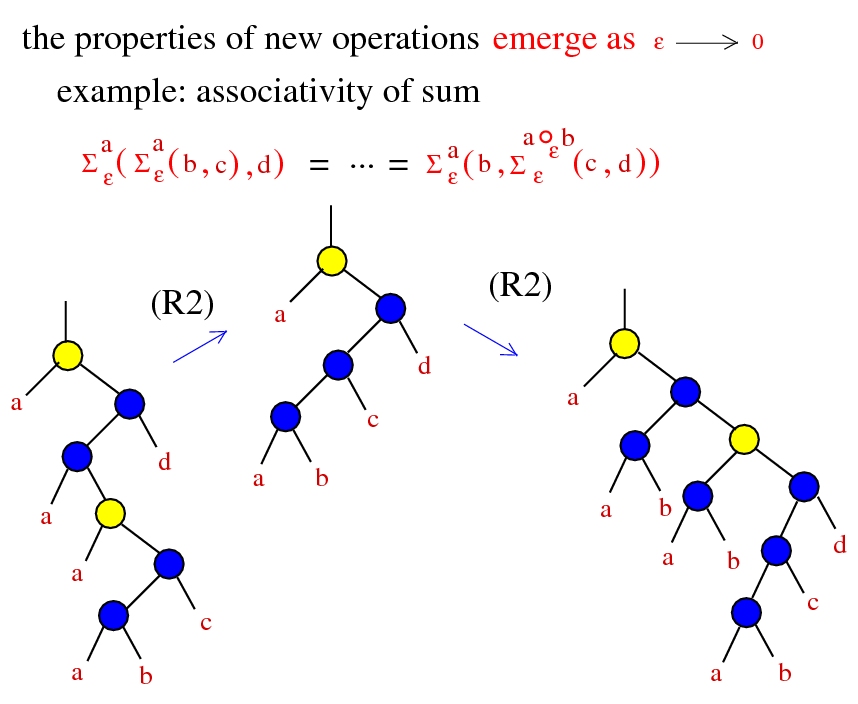
Commutativity
The operation * is commutative iff any of the following:
- - we can do the shuffle trick:
-
- - rays are semigroups, uniformly
- ∀ a, b ∈ Γ, ∃ a+b ∈ Γ, (a ⋅ x) * (b ⋅ x) = (a+b) ⋅ x
- - barycentric condition: ∀ a ∈ Γ, ∃ 1-a ∈ Γ
Commutativity
Let's denote the 3 ports of a dilation node as:
port 1: "from", port 2: "see", port 3: "as"

The operation * is commutative iff all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!
port 1: "from", port 2: "see", port 3: "as"

The operation * is commutative iff all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!
Lambda calculus
(1936, A. Church) Untyped λ calculus is a term rewrite system
Terms:
- variable: x, y, z, ...
- term:
- - variable
- - A B where A, B terms (application)
- - λx.A where x var, A term (abstraction)
Term rewrite rule:
- β-reduction: (λx.D)B → D[x=B]
(1936, A. Church) Pure λ calculus is a term rewrite system
Term rewrite rule:
- β-reduction: (λx.D)B → D[x=B]
(1971, C.P. Wadsworth, 1990, J. Lamping) graph rewrite system
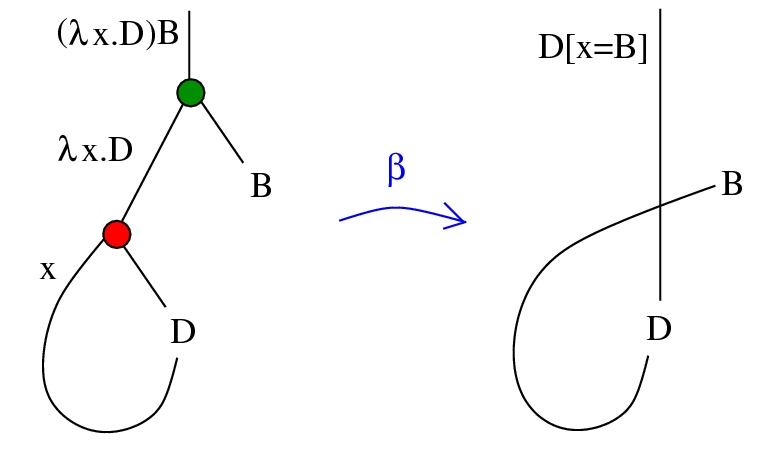
Emergent lambda
Aplication can be seen as:

(all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!)

(all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!)
Emergent lambda
Abstraction can be seen as:

(all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!)

(all the 6 permutations of ports are also dilations, with coefficients from the anharmonic group: Pure See!)
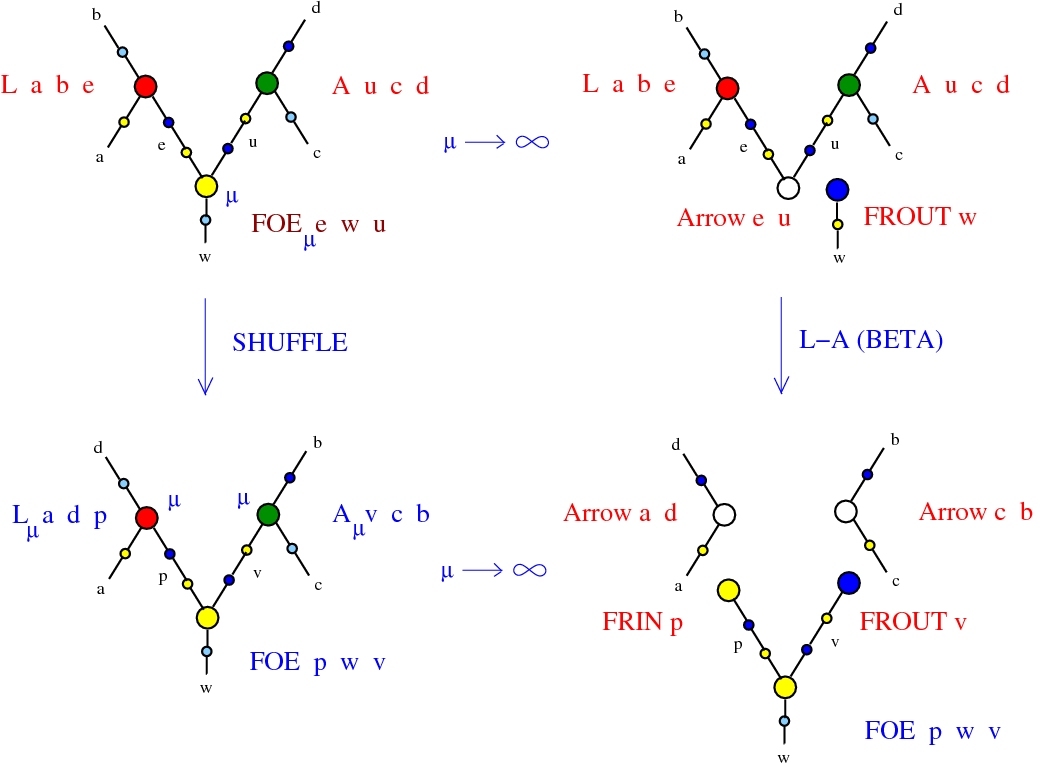
β rewrite from shuffle
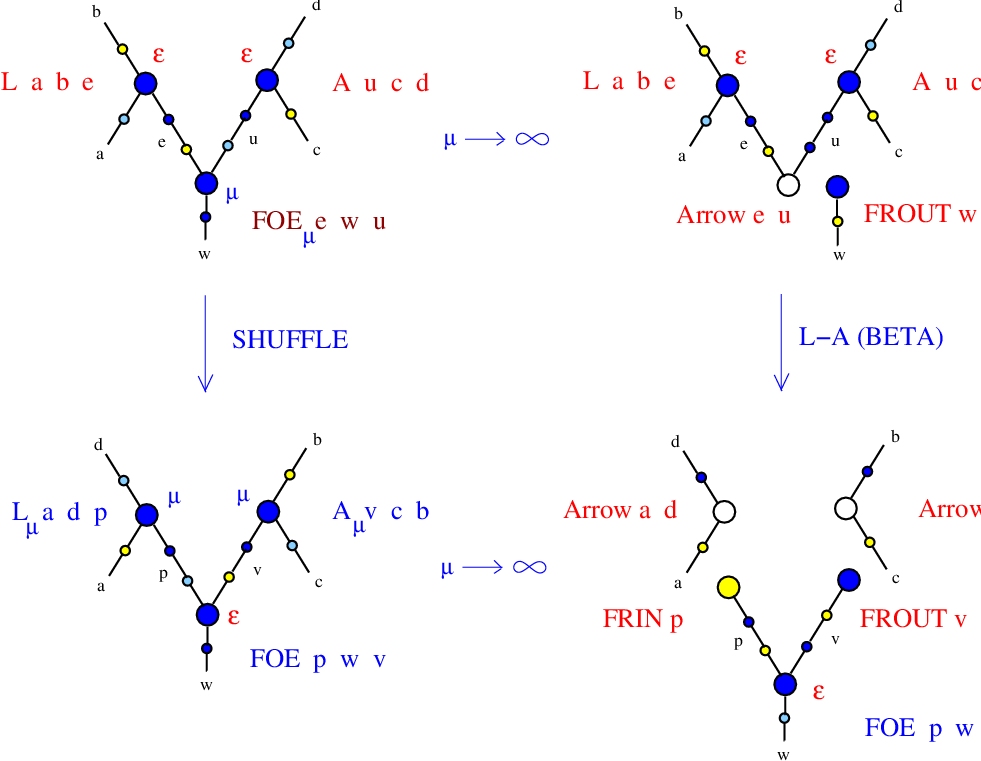
β rewrite from shuffle